• Inicio
• Buscar
• Tinglado
• Contacto
• Blogs
• Comentarios
• Admin

Tened en cuenta que al resolver un problema, el proceso que hayáis seguido para llegar al resultado es tan importante como él mismo. Por ello os pedimos que al final deis la solución que hayáis encontrado y también que expliquéis cuáles fueron las ideas más importantes que os llevaron hasta ella.

LOS MENSAJEROS DEL DESIERTO
Dos amigos del poblado más importante de una región del desierto, se han hecho con el negocio de la mensajería entre los poblados de la zona.

En llegar a cualquiera de los poblados a los que tienen que llevar mensajes tardan nueve días. Por falta de medios, tienen que llevar los mensajes a pie y aunque uno solo podría llevar los mensajes, el problema es que cada uno de ellos sólo pueden transportar comida suficiente para doce días.

Explica cómo tendrán que ingeniárselas entre los dos amigos para que uno de ellos llegue hasta su destino y ambos puedan regresar a casa sin que les falte comida para ninguno de los días. La única estrategia con la que pueden jugar, es el hecho de que la comida no es perecedera y pueden enterrar parte de ella para recogerla en el camino de vuelta.

POLÍGONOS ENCADENADOS
Observa las siguientes figuras en las que a cada polígono regular de tres, cuatro, cinco y seis lados, se le va uniendo otro del mismo tipo compartiendo un lado.

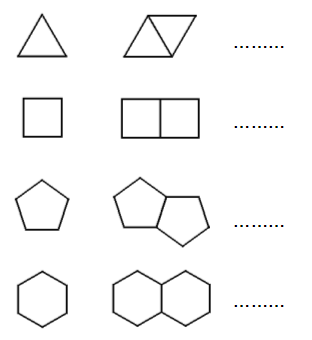
Tomando en cada caso como unidad de medida el lado del correspondiente polígono regular, recoge en una tabla cuál sería el perímetro en cada caso a medida que fuéramos uniendo más y más polígonos de la misma manera.
Obtén la expresión que nos permitirá calcular rápidamente el perímetro en el caso de que tengamos n polígonos unidos.

LAS RANAS SALTARINAS
Os proponemos que juguéis entre los tres al siguiente juego que hemos llamado ?LAS RANAS SALTARINAS?.
Para jugar, tal y como tenéis en la figura siguiente necesitáis un tablero que consiste en una fila con 7 casillas, tres fichas de un color y otras tres fichas de otro color.



El objetivo del juego es permutar las posiciones de las fichas, es decir, llevar las de la derecha a la izquierda y las de la izquierda a la derecha.
Para ello tenéis que seguir las siguientes reglas:
– Cada ficha se puede mover a la casilla contigua, si está vacía.
– Una ficha puede saltar solamente sobre otra, y no sobre más, siempre que la casilla a la que llega este vacía.
– Las fichas no pueden retroceder.
– En cada casilla solo puede haber una ficha.
– Hay que conseguir hacerlo en el menor número de movimientos posibles.
Describid de la manera más clara posible qué movimientos habéis hecho para pasar las fichas de un lado al otro siguiendo las reglas del juego.
Buscad la generalización o fórmula que nos permita averiguar la cantidad mínima de movimientos que se necesitan cuando tengamos 4 , 5 ??.. n fichas a cada lado.

MOSAICO DE ESCHER
Calculad el área de la figura con forma de pájaro que Escher diseñó para realizar este mosaico irregular.

Ver comentarios  Orden inverso  Lista  principal nuevo grupo