Enlace permanente
Máximo común divisor de dos, o más, números naturales
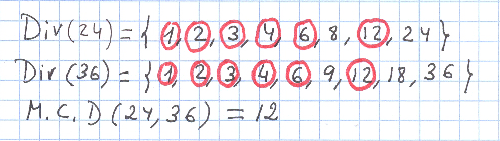
A partir de la obtención de todos los divisores de dos o más números, obtener su Máximo Común Divisor. Relacionarlo con el mínimo común múltiplo. Reglas de divisibilidad de los primeros números compuestos.
Conjunto de los divisores de un número natural
Dado un número natural cualquiera, podemos intentar encontrar todos los números naturales que lo dividen exactamente o, lo que es lo mismo, encontrar todos sus divisores.
Una vez encontrados, los podemos escribir ordenadamente de menor a mayor y formar lo que se llama el conjunto de los divisores de un número.
A diferencia del conjunto de los múltiplos que es infinito, el conjunto de los divisores es finito, es decir, tiene fin. No hay ningún número con infinitos divisores.
Para encontrar todos los divisores de un número tenemos varios métodos.
El más sencillo es buscar las parejas de números que multiplicados nos den el número inicial. Lo hacemos ordenadamente empezando por el uno y siguiendo por el dos, el tres,...
Por ejemplo:
Buscar todos los divisores de 15
1×15
2 x ?
3×5
4 x ?
Hemos encontrado cuatro divisores. Los escribimos ordenadamente de la siguiente forma:
Div(15) = { 1, 3, 5, 15 }
Se lee: los divisores de 15 son el uno, el tres, el cinco y el quince.
Buscar los divisores de 16
1×16
2×8
3 x ?
4×4
Hemos encontrado cinco divisores. Los escribimos ordenadamente:
Div(16) = { 1, 2, 4, 8, 16 }
Leemos: los divisores de 16 son el uno, el dos, el cuatro, el ocho y el dieciséis.
Buscar los divisores de 30
1×30
2×15
3×10
4 x ?
5×6
Hemos encontrado ocho divisores. Los escribimos:
Div(30) = { 1, 2, 3, 5, 6, 10, 15, 30}
Leemos: los divisores de 30 son el uno, el dos, el tres, el cinco, el seis, el diez, el quince y el treinta.
¿Cuando tenemos la certeza de que hemos acabado de buscar las parejas de factores?
Caso 1.- Cuando la pareja de números es el mismo número. Caso del 16. Llegamos al 4×4. Ya hemos acabado.
Caso 2.- Cuando llegamos a dos números consecutivos. Como en el 30. Llegamos a 5×6. Ya hemos finalizado.
Caso 3.- Cuando llegamos a una pareja de números que no son consecutivos pero los que van entre esos dos números, no funcionan. Caso del 15. Llegamos al 3×5. El único número que hay entre 3 y 5 es el 4. Pero el 4 no funciona…
Lógicamente este método es bueno cuando los números son relativamente bajos. Para números grandes hay otro método que explicaremos más adelante.
De momento puedes practicar y buscar el conjunto de los divisores de los primeros 30 números naturales.
Es muy importante que los escribas con la notación correcta:
Div(7) = { 1, 7}
Y que los leas en voz alta:
Los divisores de 7 son el uno y el siete.
Las Matemáticas son también para decirlas, para contarlas, para cantarlas,...
Por Ángel Puente en Matemáticas el 26.09.06 con 6 comentarios
![]()
![]() divisor,
divisores,
conjunto divisores,
máximo común divisor,
reglas divisibilidad números compuestos
divisor,
divisores,
conjunto divisores,
máximo común divisor,
reglas divisibilidad números compuestos
Los comentarios están cerrados.
6 comentarios
[1] Por luis el 12.03.08/17:47 ![]()
![]() Responder
Responder
Muy buenas las explicaciones. Me sirvieron demasiado. Luis, Chile, región de Valpo.
[2] Por paula piña el 09.09.08/02:23 ![]()
![]() Responder
Responder
Yo Paula Piña creo que esta página es muy muy buena porque te enseña perfectamente, por ejemplo a mi me servido de mucho y aprendí al tiro lo que necesitaba es super fácil con esta página porque tiene hasta ejemplos ![]()
![]()
[3] Por Facundo el 12.09.08/03:29 ![]()
![]() Responder
Responder
Hola: Muy buena la página me sirvió de mucho además, pude entender el m.c.d. Me gustaría que pusieras la solución de la cuadrícula porque tengo algunas dudas, sobre todo en el par (12,5).
Felicitaciones y gracias![]()
[6] Por Ma. Magdalena RamÃr el 03.04.16/22:29 ![]() Responder
Responder
Muy interesante y satisfactorio tu blog.
Disculpa y para cualquier número , solamente hay que aplicar los criterios de divisibilidad de: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 ?
Por ejemplo hay criterios de divisibilidad del 24, 47, u otros números.
Muchas gracias por el apoyo.


