Enlace permanente
Averiguar todos los divisores de un número
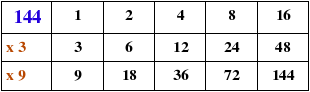
A partir de la descomposición factorial de un número, encontrar todos sus divisores.
¿Cuántos divisores tiene un número compuesto?
Un número natural o es primo o es compuesto.
En caso de que el número sea primo, éste tiene dos únicos divisores que son el 1 y el propio número.
Div(7) = {1, 7}
En caso de que el número sea compuesto, siempre tiene algún otro divisor más. De hecho es una definición, otra, de número compuesto. Un número compuesto lo es si tiene más de dos divisores.
Pero ¿cuántos divisores tiene este número compuesto? y ¿cómo saberlo?
Si un número es compuesto, se puede descomponer en producto de factores primos. Para averiguar el número de divisores, multiplicamos los exponentes de los factores incrementados todos en una unidad.
Por ejemplo, vamos a averiguar el número de divisores del 120.
Primero lo descomponemos en factores primos. Ver la entrada en la que explicamos el proceso de descomposición en factores primos.
120 = 23.3.5
Los exponentes son 3, 1 y 1:
120 = 23.31.51
luego:
Número de divisores = (3+1).(1+1).(1+1) = 4 . 2 . 2 = 16
Así que ya sabemos que tiene 16 divisores.
Encontrar todos los divisores
Ya sabemos pues, que el 120 tiene dieciséis divisores.
Pero ¿cuáles son?
Según el método ya explicado aquí, tendríamos que buscar las parejas de números que multiplicados den como resultado el 120.
Pero es un método un poco pesado. Y, si el número es mayor, más pesado todavía.
1 x 120
2 x 60
3 x 40
4 x 30
5 x 24
6 x 20
8 x 15
10 x 12
Div(120) = { 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}
El nuevo método consiste en:
1º.-Desarrollamos todas las potencias del primer factor. Como el primer factor es de exponente 3, tenemos 20, 21, 22 y 23
20 = 1
21 = 2
22 = 4
23 = 8
2º.- Estos números obtenidos se multiplican por el siguiente factor. Si este segundo factor es una potencia, tendríamos que multiplicar por cada una de los desarrollos de esta potencia. Como en este caso, el segundo factor no tiene exponente (el exponente es uno), se multiplica sencillamente por el factor.
3º.- A continuación se multiplican todos los números obtenidos (en este caso ocho) por el siguiente factor. Obtendremos otros ocho números. En total ya serán los 16 previstos. Y así sucesivamente en el caso de que hubiese más factores.
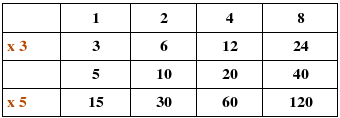
Los escribimos todos ordenadamente:
Div(120) = { 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120 }
Por Ángel Puente en Matemáticas el 15.10.06 con 15 comentarios
divisores,
factores primos,
descomposición factorial,
conjunto divisores
Los comentarios están cerrados.
15 comentarios
[1] Por Jesús Serrano el 16.10.06/17:05 
Responder
Muy bien, Angel.
Tu actividad me viene que ni pintada. En mi tutorÃa de 6º estoy con el tema del m.c.m y m.c.d. Estas tres últimas actividades tuyas las voy a utilizar con mis alumnos.
Enhorabuena.
[1.1] Por elena el 15.11.07/19:12
RESPECTO A LO DON ÁNGEL CREO QUE ERES PROFESOR NO?
YO EN EL INSTITUTO TAMBIEN ESTOY CON EL m.c.d y m.c.m LA VERDAD ES QUE LLEGABA LA HORA DE CALCULARLO Y NO TENIA NI IDEA PERO AHORA ES MUY FACIL SOLO ES PILLARLE EL TRUQUILLO TAN INSIGNIFICANTE Q TIENE QUIERO DECIR; Q ES MUY FÁCIL PERO CUESTA UN POCO.
SOLO OS DESEO SUERTE A TODOS LOS QUE LO ESTAN PASANDO COMO YO AL PRINCIPIO Y QUE TODO EL LO Q DUDEIS PREGUNTEIS
[2] Por marina el 15.11.07/19:08 
Responder
hombre a mi m parece q esto esta muy bien una pag excelente pero hay otras muchas mejores formas no estoy hablando mal d la pag. pero es q yo h aprendido t otra forma q aqui no se podria explicar (DE ESTE MODO Q YO SÉ) pero tambien está la forma de tanteo para averiguar sobre todo los numeros pequeños y de esta otra forma los grandes como ej: 1547
[2.1] Por Pepe.Gotera el 15.11.07/22:36
A ver, un traductor que nos interprete este jeroglífico.
[3] Por JOSE MANUEL el 29.11.07/18:38 Responder
Me parece muy bien explicado y sencillo de entender.
[4] Por invitado el 13.12.07/00:55 Responder
Hoy mi hija me preguntaba como saber los divisores de un número, pues no lo habian entendido en clase. Gracias a tí lo he podido hacer.
gracias
[5] Por Cecilia el 19.04.08/09:09 Responder
Me parece una pagina fenomenal. DA una vision bastante completa del tema. La utilizare con mis alumnos.
[6] Por EDUARDO CARITA V el 21.04.08/16:43 Responder
Me agradó ver esta página, y recordar algo tan útil; anoche me lo preguntaron, pero no supe hacerlo tan didáctico como en esta página, gracias y felicidades.
los seguiré visitando .......
[7] Por PsPro el 09.04.09/18:40 Responder
Excelente página, amigoo! :)
Me has ayudado en mis estudios. Recomiendo esta página a todos: fácil de entender y con ejercicios.
Todo lo resume en una palabra : GRACIAS
[8] Por frank el 10.07.09/17:54 Responder
Están muy buenos los consejos que publicas y al fin pude entender y más facil, práctico y rapido. Gracias.
[11] Por viviana el 14.06.11/16:33 Responder
necesito saber lo divisores urgente de 1,2,3,4,5,6,7,8,9,10,12,18,24,48 y100
[12] Por alvaro el 05.07.11/03:43 Responder
Hola un especial agradecimiento a quienes están apoyando esta maravillosa página, me ha servido de mucho para explicarle matemáticas a mis hijos. Les agradezco su valiosa y desinterada ayuda. Suerte les deseo.
[13] Por Euge el 08.08.15/00:35 Responder
Si tengo un número A, producto de dos factores primos cualquieras, cuál es el número de divisores de A? Cómo puedo saberlo? Por favor, necesito ayuda! Gracias
