Enlace permanente
Reglas de divisibilidad
Actualizado el 28.08.07/18:39
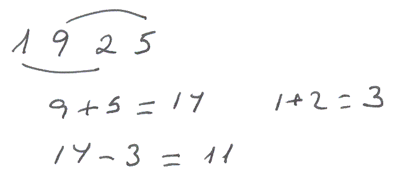
La relación ser divisible por y la relación ser múltiplo de es como la relación de parentesco entre personas "ser tío de" y "ser sobrino de":
Si Juan es tío de Pedro, Pedro es sobrino de Juan.
Si 6 es múltiplo de 2, entonces, 2 es divisor de 6.
Si 9 no es múltiplo de 5, entonces, 5 no es divisor de 9
Saber si un determinado número es divisible por otro, es muy importante. Sobre todo, es importante saber si un determinado número natural es divisible por un determinado número primo. ¿Por qué es tan importante? Pues porque los números que no son primos, es decir, los compuestos, se pueden descomponer en producto de primos y esta descomposición factorial es muy necesaria para resolver múltiples problemas numéricos o algebraicos.
Regla de divisibilidad por 2
Observa los múltiplos de 2:4; 6; 8, 10; 12; 14; 16; 18; 20; 22; 24; 26; 28;...
Recuerda lo fácil que fue eliminar los múltiplos de 2 en la Criba de Eratóstenes. ¿Por qué era tan fácil? ¿Qué tienen en común todos los múltiplos de 2? ¿En qué acaba todo múltiplo de 2?
Regla de divisibilidad por 3
Observa los múltiplos de 3:6; 9; 12; 15; 18; 21; 24; 27; 30; 33; 36; 39; 42;...
Haz lo siguiente: Suma las cifras de cada número y apunta el resultado:
12 --> 1 + 2 = 3
15 --> 1 + 5 = 6
18 --> 1 + 8 = 9
21 --> 2 + 1 = 3
24 --> 2 + 4 = 6
¿Has observado ya algo?
Si todavía no... sigue sumando las cifras de los siguientes múltiplos.
Regla de divisibilidad por 5
¿Recuerdas lo fácil que fue eliminar en la Criba de Eratóstenes a los múltiplos de 5?¿Por que era tan fácil?
10; 15; 20; 25; 30; 35; 40; 45; 50;...
¿Qué pasa con la cifra de las unidades de todo múltiplo de 5? Fácil ¿no? Igual de fácil que fue, cuando éramos pequeños, aprendernos la tabla del 5...
Regla de divisibilidad por 7
Esto es mucho más difícil.Para saber si un determinado número es divisible por 7 pues hacemos la división y observamos si el resto es cero...
Que es cero.... El número es divisible por 7
Que no lo es... El número no es divisible por 7
Esto evidentemente, no es ninguna regla, es el concepto inicial de divisibilidad aplicable a cualquier primo o no primo...
Pero hay una regla muy curiosa que no todo el mundo conoce. Te la explico:
Paso 1.- Eliminas la cifra de las unidades del número.
Paso 2.- Al número que queda, le restas el doble de la cifra eliminada.
Paso 3.- Repites los pasos 1 y 2 hasta que llegues a un número de una cifra o de dos pero que la cifra de las decenas sea menor que el doble de la cifra de las unidades...
Y observas el resultado: Si el número final es cero, siete u otro múltiplo de 7, es que el número es divisible.
En caso de que no salga un múltiplo de 7, el número no es divisible por 7.
Pongamos un ejemplo:
¿Es 1652 divisible por 7?
Paso 1.- Eliminamos la cifra de las unidades. El número que queda es el 165
Paso 2.- Al 165 le restamos el doble de 2, es decir, 4:
165 - 4 = 161
Repetimos el paso 1.- Eliminamos la cifra de las unidades. El 1. El número que queda es 16
Repetimos el paso 2.- A 16 le restamos el doble de 1, es decir, 2:
16 - 2 = 14
Como 14 es un múltiplo de 7, el número inicial, el 1652 es divisible por 7
Otro ejemplo:
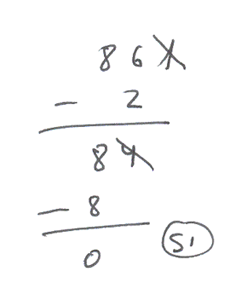
El 861 es divisible por 7.
Regla de divisibilidad por 11
Fíjate en los múltiplos de 11:22; 33; 44; 55; 66; 77; 88; 99; 110; 121; 132; 143; 154;...
En el caso de que tenga dos cifras... ¿qué pasa?
En el caso de que el número tenga tres cifras... Suma la primera y la tercera y observa el resultado...
Ahora observa estos múltiplos de 11 de cuatro cifras:
1100; 1111; 1122; 2332; 3586;
Ponte tú otros ejemplos y observa qué pasa si sumas las cifras colocadas en lugar par y sumas las cifras colocadas en lugar impar...
Esta regla se enuncia así:
Un número es divisible por 11 cuando al sumar las cifras colocadas en lugar par y restarlo de la suma de las cifras colocadas en lugar impar (o viceversa) se obtiene cero, once u otro múltiplo de once.
Reglas de divisibilidad por otros números no primos
Aquí tienes explicadas las reglas de divisibilidad por los primeros números compuestos (4, 6, 8, 9 y 10).Comprueba tus conocimientos.
Antes de empezar a resolver el test pincha en Instrucciones. Este test se compone de dos bloques de cinco emparejamientos cada uno. Javascript original de Alejandro ValeroA continuación puedes aplicar las reglas de divisibilidad a los 6 siguientes números de cuatro cifras escribiendo en cada caso si o no (con minúsculas, sin acento) en cada casilla según corresponda. Cuando acabes pulsa el botón comprobar para ver si lo has hecho bien.
Por Ángel Puente en Matemáticas el 18.05.06 con 31 comentarios
reglas de divisibilidad,
criterios de divisibilidad,
múltiplos,
divisores,
primos,
compuestos,
números naturales
Los comentarios están cerrados.
31 comentarios
[1.1] Por Pepe Yepes el 20.08.06/20:07 
Hola. Un número es divisible por 6 si cumple simultáneamente las reglas de divisibilidad por 2 y por 3. En cuanto al 4, un número es divisible por 4 si acaba en 0, en 4 o en 8 y su cifra de decenas es par, o acaba en 2 o en 6 y su cifra de decenas es impar.
[1.2] Por isa el 21.10.10/22:34
Son muy fáciles: la del 4 es si sus dos últimas cifras son un multiplo de 4
y la del 6 : si es múltiplo de 2 y 3 al mismo tiempo
[3] Por ALBERTO VAQUERO VERA el 05.09.06/15:32 Responder
21ALBVAQ@YAHOO.COM.MX. NECESITO UNA RESPUESTA SOBRE LA DIVISIBILIDAD ENTRE CERO
[3.1] Por Ángel Puente el 05.09.06/19:49
Hola Alberto. El cero es un número muy especial. Tanto es asÃ, que los romanos, por ejemplo, no disponÃan de esta cifra... Si el número es la representación de una cantidad... el cero es la negación de la cantidad. AsÃ, por ser un número tan especial, ocurren muchas cosas con este número que no ocurren con los demás. Por ejemplo la división. Se dice que no se puede dividir ningún número entre cero. La división no es posible. Asà no podemos hablar de reglas de divisibilidad para el cero. Espero haberte ayudado.
[3.2] Por soni el 02.12.07/20:52
la del 0 no se pone nunca no ???????
[4] Por Gabriela Caballero el 15.09.06/15:13 Responder
Hola a todos!!!Esto va para el creador de esta genial pagina web.:
Me encanta esta web por q puedo estudiar para el cole, esta buenisima. Me gustan los ejercicios de matematica para practicar para la escuela. Pero me gustarÃa que en el segundo, en elq hay q colocar si o no según q numero sea, cuando te equivocas, te digan en cual te equivocaste, por q asà yo nunca lo pude terminar.
Muchas gracias
Gaby 
[5] Por Daniel el 27.09.06/04:20 Responder
Pienso que estas explicaciones estan muy bien , me habìa perdido buscando como saber si algun numero esdivisble entre 7 y 11 y por fin lo encontre. Todo esta muy bien hasta los ejercicios e insisto todo bien hecho y explicado, y por ultimo una felicitacion al genio (a) que hizo esto
no le entendi nada
[7] Por Lilia el 01.11.06/21:12 Responder
Los felicito por su página, es de suma utilidad, está muy bien explicado, y los juegos me parecen padrÃsimos...sigan asà y felicidades.
Lilia MartÃnez Reyes
[8] Por G@By el 03.03.07/15:20 Responder
HoLaAaAaA!!
EsTa eS La pRiMeRa VeZ q UsO eStA pAgInA, y Es De Lo MeJoR...
fElIcItO aL gEnIo Q hIzO eStA pAgInA...
[10] Por Nicolas Meisenbichle el 15.03.07/22:42 Responder
compadre tengo una duda espero que me puedas ayudar...que diferencia hay entre un angulo adyasente y uno suplementario ¿?
- Nicolás, introduciendo en tu buscador web, Google por ejemplo, las palabras referidas a tus dudas, seguro que encuentras respuestas. Por ejemplo:
ángulos adyacentes
ángulos suplementarios
Vigila la ortografÃa 
[11] Por José Miguel el 25.10.07/23:34 Responder
Hola a todos!!! Gracias por la información Me salvaron un deber. Si alguien tiene tiempo libre, entonces vayan a http://www.clubpenguin.com/ y descubran algo divertido!!!! P.S.: El cero trabaja como 0.
[12] Por soni el 02.12.07/20:49 Responder
esta pagina es genial yo todavia estoy dando las reglas de divisibilidad y me lo se bien
el lunes tengo examen y me parece k voy mu bien preparada
xao
[13] Por pablo el 07.06.08/17:59 Responder
Agradezco al que fue la idea y nos ayuda mucho a nosostros los estudiantes,
me gustaría saber más sobre la divisibilidad del 15-16 y mucho mejor si fuera con ejemplos.
[14] Por maria el 15.09.08/14:17 Responder
Hola, la página esta muy buena. Gracias, me ayudas un montón.
[15] Por s el 17.09.08/22:47 
Responder
Muy buena la página. Excelente la explicación de la regla del 7. Gracias.
[16] Por lili el 22.11.08/19:00 Responder
Hola!
necesito las reglas de divisibilidad del 13 y del 17...
me ayudariareis mucho.
gracias. =)
[16.1] Por jose el 08.01.09/13:18
Por las pruebas que yo he hecho, parece que existe siempre una fórmula que permite predecir si un número es divisible por otro primo.
Por ejemplo:
los múltiplos de 11 de 2 cifras (ab) cumplen que: ((1*a)-b) mod 11 = 0 ó lo que es lo mismo
1*a - b = múltiplo de 11 o cero
los múltiplos de 13 de 2 cifras (ab) cumplen que: ((3*a)-b)mod 13 = 0
los múltiplos de 17 de 2 cifras (ab) cumpen que: ((7*a)-b) mod 17 = 0
los múltiplos de 19 de cifras (ab) cumplen que: ((9*a)-b) mod 19= 0
y así sucesivamente.
Parece que existe un cierto orden, además que para números de más dígitos parece funcionar de modo iterativo.
[17] Por jose el 08.01.09/13:16 Responder
Las reglas de divisibilidad son fáciles de aplicar en números construídos con factores primos pequeños, pero cuando se trata de buscar factores primos más elevados el problema se complica, por ejemplo el número 221 (formado por los primos 13*17).
Podrías decirme si existe una regla general para la factorización en números primos o prueba de la divisibilidad.
Por las pruebas que yo he hecho, parece que existe siempre una fórmula que permite predecir si un número es divisible por otro primo.
Por ejemplo:
los múltiplos de 11 de 2 cifras (ab) cumplen que: ((1*a)-b) mod 11 = 0 ó lo que es lo mismo
1*a - b = múltiplo de 11 o cero
los múltiplos de 13 de 2 cifras (ab) cumplen que: ((3*a)-b)mod 13 = 0
los múltiplos de 17 de 2 cifras (ab) cumplen que: ((7*a)-b) mod 17 = 0
los múltiplos de 19 de 2 cifras (ab) cumplen que: ((9*a)-b) mod 19= 0
y así sucesivamente.
Parece que existe un cierto orden, además que para números de más dígitos parece funcionar de modo iterativo.
[18] Por Yannick el 25.03.09/21:32 Responder
Me ayudaste mucho con esto, voy a aprobar todos los exámenes y aparte me gusta que haya gente buena en este mundo que piense en otros.
[19] Por Claudia el 29.03.09/00:05 Responder
El famoso cuadro estaba malo!!.... como me decia que estaba incorrecto si lo hice como 1000 veces y me decia lo mismo y depues lo hice con calculadora y de nuevo me salia incorrecto... deben arreglarlo porque al parecer no estaba programado para poner correcto... solo eso... la pagina esta buenisima!!! mil felicitaciones me ayudo mucho para mis tareas e investigaciones! gracias.
[20] Por Claudio el 23.06.09/23:25 Responder
Sos muy didáctico. Acabo de enseñarle a mi hijo la regla de divisibilidad por 7 basado en tu explicación.
Felicitaciones y gracias
Claudius
[21] Por isa el 21.10.10/22:36 Responder
Pues a mi no me gustan nada las mates las odio!!! y mañana tengo un examen!!!
========
Pues estudia 
.
[22] Por natalia el 06.01.11/14:07 Responder
A mí me gustan las mates lo que pasa que me di cuenta que me cuestan bastante pero para areglarlo solo hay que ponerse a estudiar y me di cuenta cuando llege a primero de la eso hay si que tienes que estudiar para aprobar xao hasta pronto
[23] Por valentina el 04.05.11/01:28 Responder
me gusto mucho las pagina, pero hay partes que uno se pierde
[24] Por david el 02.08.11/06:29 Responder
Exelente. ¿Cómo sería para numeros primos más altos?
¿De pronto existirá un algoritmo para saber si un número es primo o no?
[25] Por Lauren el 17.10.12/19:49 Responder
No es la primera vez que utilizo esta página y me gusta.
Os habréis preguntado porque mi nombre parece Ingles ¿no?, 1Es Inglés y 2Es que mis padres son Ingleses y fui a España de pequeña, y aprendí español e inglés pero ahora estoy otra vez en Ontario, Canadá.
[26] Por maria alvarado el 10.04.15/00:24 Responder
Profesor muy interesante esta página. Desearía que me brindara orientación sobre la explicación del siguiente ejercicio:
Calcula la suma de los posibles valores de "a" en: 4573a=3
Solucion: 4+5+7+3a = 3 a+19=3 {0, 3, 6, 9, 12, 15, 18}
a= 2, 5, 8 Luego: 2+5+8 = 15
Respuesta: La suma es 15.
¿De dónde salen los numeros 2, 5, 8? ¿por qué se los tiene que utilizar?
