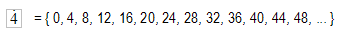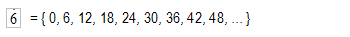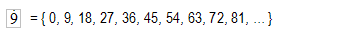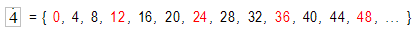Conjunto de los múltiplos de un número.
Dado un número cualquiera, podemos escribir ordenadamente sus primeros múltiplos. Se suele escribir así:

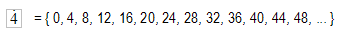
Y se lee: los múltiplos de 4 son el cero, el cuatro, el ocho, el doce, etc.
Indicando que los múltiplos de cuatro continúan, que “no se acaban nunca”, que son infinitos.
Observa el punto colocado encima del número. Es la notación para indicar “los múltiplos de...”
Veamos ahora el conjunto de los múltiplos de otro número cualquiera.
Por ejemplo, el 6:

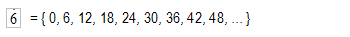
Los múltiplos de 6 son el cero, el seis, el doce, el dieciocho, el veinticuatro, etc.
Veamos ahora el conjunto de los múltiplos de 9:

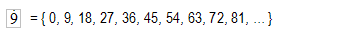
Los múltiplos de 9 son el cero, el nueve, el dieciocho, etc.

Actividad:
Escribe con la notación correcta el conjunto de los múltiplos de otros cinco o seis números naturales. Practica su lectura en voz alta.

Mínimo común múltiplo de dos o más números.
Ahora podemos comparar los múltiplos obtenidos en el ejercicio anterior.
Por ejemplo, vamos a comparar los múltiplos de 4 y los múltiplos de 6, fijándonos en los números que son múltiplos de los dos. Los marcamos con otro color:


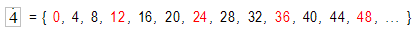
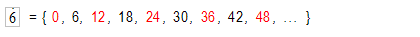
Lógicamente como los múltiplos son infinitos también lo son los múltiplos comunes de estos dos. Aunque no estén explícitamente escritos, puedes observar que si la lista la continuamos, siguen apareciendo múltiplos repetidos, múltiplos comunes de los dos números.
Pues bien, de todos estos múltiplos comunes el que más nos interesa es el más pequeño de todos ellos pero sin tener en cuenta al cero.
Llamamos mínimo común múltiplo de dos o más números naturales, a otro número natural que es múltiplo de los dos (o de todos los que sean) y, de todos los posibles, es el más pequeño sin contar el cero. En nuestro caso es el 12. Escribimos:
m.c.m.(4 , 6) = 12
Y leemos: El mínimo común múltiplo de 4 y de 6 es 12

Actividad
Averigua los mínimos comunes múltiplos de cada una de las parejas propuestas. Una vez que lo hayas averiguado, arrastra el resultado correcto con cada una de las parejas que le corresponda.