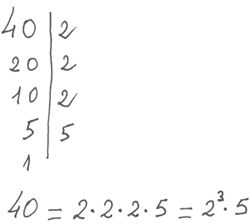Hasta ahora, el proceso que hemos visto para la descomposición factorial de un número, era, básicamente, el proceso de "romper" en producto de otros dos y, si no son primos, volver a romper en producto de otros dos... método perfectamente válido para números relativamente pequeños o que podamos descomponer "de cabeza".
De todas formas, estos métodos, son los mejores pues son los que más cerca están de los conceptos...
Pero, si el número es grande, el método no es muy práctico...
Hay que buscar un método que permita enfrentarnos con garantía de éxito y con cierta comodidad al proceso de descomponer en factores primos cualquier número natural por grande que sea.
El método que vamos a explicar es el denominado de las divisiones sucesivas.
Se trata de ir dividiendo al número, ordenadamente, por los primeros primos por los que sea divisible. Empezando por el 2 y no pasando al siguiente hasta que no se acabe...
Es decir, dividimos el número por el primer primo que sea divisible.
Se obtiene un cociente.
Este cociente se vuelve a dividir por el mismo primo (si es divisible).
Si no es divisible, se pasa al siguiente primo.
Se obtiene otro cociente.
Se vuelve a dividir por el mismo primo (si es divisible).
Si no lo es, se pasa al siguiente primo.
Así sucesivamente hasta llegar a un último cociente que sea primo.
Se divide (aunque no sería necesario) por este último divisor primo para obtener el 1 como cociente.
El número inicial será el producto de todos sus divisores primos.
Lo hacemos con un ejemplo:
Supongamos que queremos descomponer el número 567.
No es divisible por 2 --> No acaba en cifra par.
Sí lo es por 3 --> 5 + 6 + 7 = 18 y 18 es múltiplo de 3.
Quizá lo sea más de una vez...
También lo es por 7, pues 56 - 14 = 42 y 42 es múltiplo de 7.
Como ves las reglas o criterios de divisibilidad son un recurso frecuentemente empleado...
El proceso podría presentarse así:
Observa que, a pesar de mi reflexión inicial sobre los primos por los que puede ser divisible el número, no ha hecho falta dividirlo por 7. El 7 ha aparecido como último divisor. Lo que anima a grabarse las reglas principales:
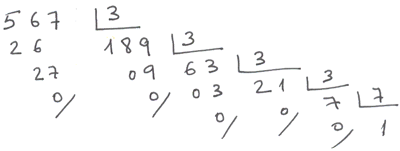
- Lo importante es empezar por el primer primo por el que el número sea divisible y...
- No pasar al siguiente hasta que no estemos seguros de que ya se ha "agotado" el primo en el que estamos trabajando.
Una vez, realizado el proceso, se presentan los resultado finales:
Observa que ya hemos empezado a utilizar la escritura en forma de potencia. Es la forma habitual de presentar los resultados.
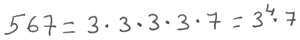
Para finalizar, este proceso se suele resumir en una presentación un poco más sencilla. Se trata, simplemente, de ahorrarnos todos los datos intermedios de cada división. Lo único importante es el divisor y el cociente. Pues bien, lo podemos realizar de la siguiente forma:
Y, de forma habitual, se suelen presentar directamente los resultados en forma de potencia:

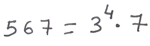
ACTIVIDAD PROPUESTA

Te planteamos la descomposición factorial de los seis números de cuatro cifras que te propusimos en la actividad de las reglas de divisibilidad.
Se trata pues, de que intentes descomponer en factores primos los números:
2310; 1470; 2970; 2197; 1694 y 1155.
Hazlo primero con lápiz y papel y, después, comprueba tus resultados con los que te proponemos aquí debajo.
Arrastra cada descomposición factorial de la columna derecha a su correspondiente número compuesto de la columna izquierda.
Cuando hayas acabado pulsa el botón COMPROBAR.
Si quieres repetirlo dale al botón Actualizar de tu navegador.