XIV Olimpiada Matemática 2º E.S.O. Grupo

Problemas que se han propuesto para la resolución en grupo
Fase semifinal de la XIV Olimpiada Matemática para 2º de la E.S.O. de la Comunidad de Madrid. Miércoles, 26 de abril de 2006. Prueba de grupo.
Esta misma mañana han tenido lugar estas pruebas.
En El Tinglado nos apresuramos a publicarlas. Esta vez no hay ningún test, ninguna pista, ninguna explotación didáctica de la situación problemática… Entre otras cosas, porque no ha habido tiempo material. Nos gustaría mucho que los propios alumnos que han participado en las pruebas, nos comentasen sus procesos en la búsqueda de las soluciones…
(10/02/07) Actualización: Colocadas las soluciones.
Tened en cuenta que al resolver un problema, el proceso que hayáis seguido para llegar al resultado es tan importante como él mismo. Por ello os pedimos que al final deis la solución que hayáis encontrado y también que expliquéis cuáles fueron las ideas más importantes que os llevaron hasta ella.
JUGANDO CON PALILLOS
Averigua cuál es la cantidad mínima de palillos que se necesitan para formar 6 cuadrados.
Dibuja cómo los colocarías y haz una descripción de la situación.
EL REPARTO
El Departamento de actividades extraescolares de tu centro, ha organizado una excursión a la sierra para este fin de semana a la que vais a asistir los 16 alumnos y alumnas de la clase, un profesor y una profesora.
Para cenar el primer día, entre otraqs cosas, se ha comprado una lata grande de salchichas en la que entran 30 salchichas.
Evidentemente, tenemos que repartirlas de modo que todos recibamos la misma cantidad. ¿Cuál será el número mínimo de cortes que tendremos que hacer? ¿Qué cantidad de salchichas tendremos cada uno en el plato?
PENTAMINÓS
Llamamos “Pentaminós” a todos aquellos polígonos que sobre una trama de puntos ortogonal como la que tienes más abajo. pueden formarse uniendo cinco cuadrados por los lados.

Tomando como unidad de área (u.d.a.) la del cuadrado más pequeño que puede formarse sobre la trama de puntos y como unidad de longitud (u.d.l.) el lado de dicho cuadrado, dibuja todos los Pentaminós que puedas.
Nota: Consideraremos Pentaminós iguales todos aquellos que puedan superponerse aplicándoles un movimiento cualquiera, es decir, una traslación, un giro o dándoles la vuelta (reflexión)

Calcula además el perímetro de todos los pentominós que construyas. ¿Qué conclusiones puedes sacar de tu estudio?
Nota 2: A continuación tienes otra trama de puntos para que hagas tus razonamientos.
LOS BARRILES
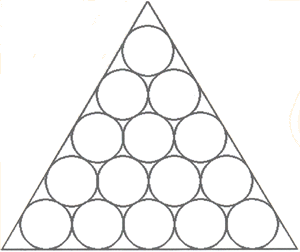
A continuación te mostramos la vista en planta de un contenedor con forma de triángulo equilátero en el que se almacenan barriles de diferentes compuestos químicos.
Para diferenciar unos barriles de otros están pintados de diferente color. Hay 5 rojos, 5 amarillos y 5 verdes. Resulta peligroso que dos barriles del mismo compuesto químico estén próximos entre sí, de ahí que de lo que se trata es de colocar los barriles de forma que la distancia mínima entre dos barriles del mismo compuesto sea lo más grande posible.
Indica sobre la figura cómo los colocarías.
SOLUCIONES
JUGANDO CON PALILLOS
Averigua cuál es la cantidad mínima de palillos que se necesitan para formar 6 cuadrados.
Dibuja cómo los colocarías y haz una descripción de la situación.
Dado que el enunciado no indica que los cuadrados tengan que ser iguales, podemos asegurar como se ve en la figura siguiente que nos bastan 9 palillos para formar 6 cuadrados.
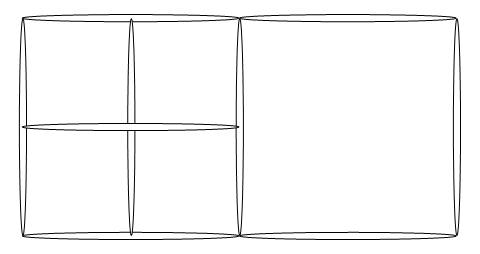
Dos de ellos tendrán como lado la longitud de cada uno de los palillos y tendremos cuatro cuyo lado será la mitad de dicha longitud.
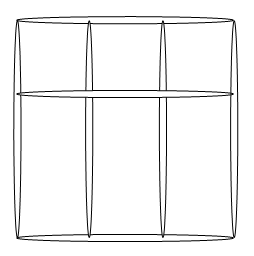
Sin embargo, existe otra posible solución que nos permite obtener los 6 cuadrados empleando únicamente 7 palillos.
Uno de ellos tendrá como lado la longitud de cada uno de los palillos, habrá tres cuyo lado será la tercera parte de dicha longitud y por último aparecerán dos cuadrados más que se superponen y que tendrán como lado dos terceras partes de la longitud de cada palillo.
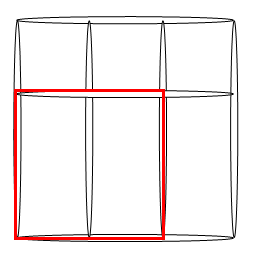
Señalamos con rojo uno de estos dos cuadrados que tienen como lados las dos terceras partes de la longitud del palillo:
EL REPARTO
El Departamento de actividades extraescolares de tu centro, ha organizado una excursión a la sierra para este fin de semana a la que vais a asistir los 16 alumnos y alumnas de la clase, un profesor y una profesora.
Para cenar el primer día, entre otraqs cosas, se ha comprado una lata grande de salchichas en la que entran 30 salchichas.
Evidentemente, tenemos que repartirlas de modo que todos recibamos la misma cantidad. ¿Cuál será el número mínimo de cortes que tendremos que hacer? ¿Qué cantidad de salchichas tendremos cada uno en el plato?


PENTAMINÓS
Llamamos “Pentaminós” a todos aquellos polígonos que sobre una trama de puntos ortogonal como la que tienes más abajo. pueden formarse uniendo cinco cuadrados por los lados.

Tomando como unidad de área (u.d.a.) la del cuadrado más pequeño que puede formarse sobre la trama de puntos y como unidad de longitud (u.d.l.) el lado de dicho cuadrado, dibuja todos los Pentaminós que puedas.
Nota: Consideraremos Pentaminós iguales todos aquellos que puedan superponerse aplicándoles un movimiento cualquiera, es decir, una traslación, un giro o dándoles la vuelta (reflexión)

Calcula además el perímetro de todos los pentominós que construyas. ¿Qué conclusiones puedes sacar de tu estudio?
Nota 2: A continuación tienes otra trama de puntos para que hagas tus razonamientos.
Existen exactamente 12 pentominós tal como se muestran en esta figura:
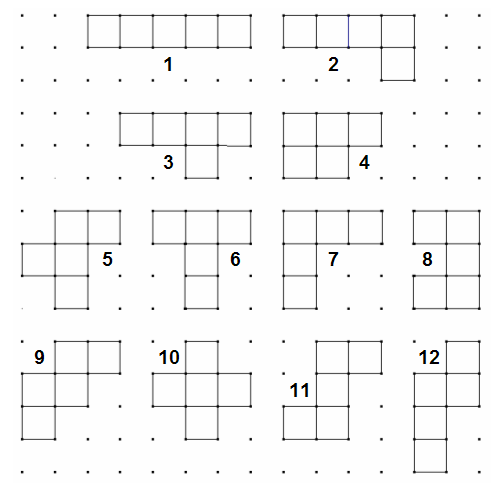
La siguiente tabla muestra que, como es evidente el área de todos los Pentaminós es la misma, pero su perímetro no lo es:
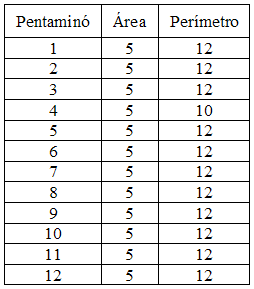
LOS BARRILES
A continuación te mostramos la vista en planta de un contenedor con forma de triángulo equilátero en el que se almacenan barriles de diferentes compuestos químicos.
Para diferenciar unos barriles de otros están pintados de diferente color. Hay 5 rojos, 5 amarillos y 5 verdes. Resulta peligroso que dos barriles del mismo compuesto químico estén próximos entre sí, de ahí que de lo que se trata es de colocar los barriles de forma que la distancia mínima entre dos barriles del mismo compuesto sea lo más grande posible.
Indica sobre la figura cómo los colocarías.

Teniendo en cuenta las indicaciones del enunciado, parece lógico que comencemos la colocación de los barriles de la forma siguiente:
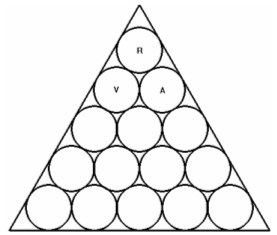
Puesto que debemos separar lo máximo posible los barriles del mismo color, podríamos pensar que una buena colocación podría ser la siguiente:
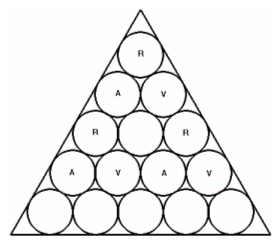
Sin embargo, esta disposición que posibilita una separación máxima a priori en-tre barriles del mismo color, en el momento que tratemos de colocar el resto, nos lleva a la situación de que irremediablemente otros barriles del mismo compuesto queden unos junto a otros.
Por lo tanto, pensando en una estrategia válida a largo plazo, el modo de colocar los siguientes tres barriles será el que se muestra a continuación:
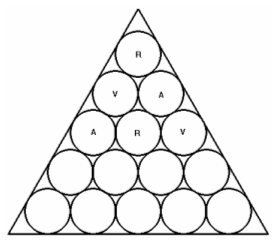
En este momento puede llegar a advertirse ya cierto patrón en la ubicación óptima de los barriles con lo que las siguientes figuras ilustran el modo en el que tendremos que seguir colocándolos de modo que se cumpla la premisa impuesta.
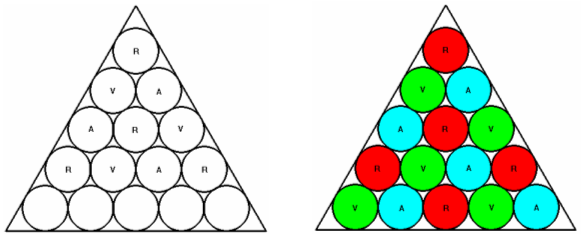
Texto de Ángel Puente - 26.04.06URL del artículo: http://www.tinglado.net/?id=xiv-olimpiada-matematica-2-eso
(El tinglado - http://www.tinglado.net - Con licencia de Creative Commons)

















