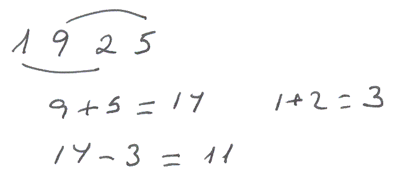La relación ser divisible por y la relación ser múltiplo de es como la relación de parentesco entre personas "ser tío de" y "ser sobrino de":
Si Juan es tío de Pedro, Pedro es sobrino de Juan.
Si 6 es múltiplo de 2, entonces, 2 es divisor de 6.
Si 9 no es múltiplo de 5, entonces, 5 no es divisor de 9
Saber si un determinado número es divisible por otro, es muy importante. Sobre todo, es importante saber si un determinado número natural es divisible por un determinado número primo. ¿Por qué es tan importante? Pues porque los números que no son primos, es decir, los compuestos, se pueden descomponer en producto de primos y esta descomposición factorial es muy necesaria para resolver múltiples problemas numéricos o algebraicos.
Regla de divisibilidad por 2
Observa los múltiplos de 2:4; 6; 8, 10; 12; 14; 16; 18; 20; 22; 24; 26; 28;...
Recuerda lo fácil que fue eliminar los múltiplos de 2 en la Criba de Eratóstenes. ¿Por qué era tan fácil? ¿Qué tienen en común todos los múltiplos de 2? ¿En qué acaba todo múltiplo de 2?
Regla de divisibilidad por 3
Observa los múltiplos de 3:6; 9; 12; 15; 18; 21; 24; 27; 30; 33; 36; 39; 42;...
Haz lo siguiente: Suma las cifras de cada número y apunta el resultado:
12 --> 1 + 2 = 3
15 --> 1 + 5 = 6
18 --> 1 + 8 = 9
21 --> 2 + 1 = 3
24 --> 2 + 4 = 6
¿Has observado ya algo?
Si todavía no... sigue sumando las cifras de los siguientes múltiplos.
Regla de divisibilidad por 5
¿Recuerdas lo fácil que fue eliminar en la Criba de Eratóstenes a los múltiplos de 5?¿Por que era tan fácil?
10; 15; 20; 25; 30; 35; 40; 45; 50;...
¿Qué pasa con la cifra de las unidades de todo múltiplo de 5? Fácil ¿no? Igual de fácil que fue, cuando éramos pequeños, aprendernos la tabla del 5...
Regla de divisibilidad por 7
Esto es mucho más difícil.Para saber si un determinado número es divisible por 7 pues hacemos la división y observamos si el resto es cero...
Que es cero.... El número es divisible por 7
Que no lo es... El número no es divisible por 7 :smile:
Esto evidentemente, no es ninguna regla, es el concepto inicial de divisibilidad aplicable a cualquier primo o no primo...
Pero hay una regla muy curiosa que no todo el mundo conoce. Te la explico:
Paso 1.- Eliminas la cifra de las unidades del número.
Paso 2.- Al número que queda, le restas el doble de la cifra eliminada.
Paso 3.- Repites los pasos 1 y 2 hasta que llegues a un número de una cifra o de dos pero que la cifra de las decenas sea menor que el doble de la cifra de las unidades...
Y observas el resultado: Si el número final es cero, siete u otro múltiplo de 7, es que el número es divisible.
En caso de que no salga un múltiplo de 7, el número no es divisible por 7.
Pongamos un ejemplo:
¿Es 1652 divisible por 7?
Paso 1.- Eliminamos la cifra de las unidades. El número que queda es el 165
Paso 2.- Al 165 le restamos el doble de 2, es decir, 4:
165 - 4 = 161
Repetimos el paso 1.- Eliminamos la cifra de las unidades. El 1. El número que queda es 16
Repetimos el paso 2.- A 16 le restamos el doble de 1, es decir, 2:
16 - 2 = 14
Como 14 es un múltiplo de 7, el número inicial, el 1652 es divisible por 7
Otro ejemplo:
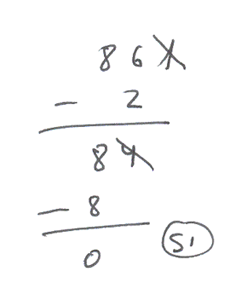
El 861 es divisible por 7.
Regla de divisibilidad por 11
Fíjate en los múltiplos de 11:22; 33; 44; 55; 66; 77; 88; 99; 110; 121; 132; 143; 154;...
En el caso de que tenga dos cifras... ¿qué pasa?
En el caso de que el número tenga tres cifras... Suma la primera y la tercera y observa el resultado...
Ahora observa estos múltiplos de 11 de cuatro cifras:
1100; 1111; 1122; 2332; 3586;
Ponte tú otros ejemplos y observa qué pasa si sumas las cifras colocadas en lugar par y sumas las cifras colocadas en lugar impar...
Esta regla se enuncia así:
Un número es divisible por 11 cuando al sumar las cifras colocadas en lugar par y restarlo de la suma de las cifras colocadas en lugar impar (o viceversa) se obtiene cero, once u otro múltiplo de once.
Reglas de divisibilidad por otros números no primos
Aquí tienes explicadas las reglas de divisibilidad por los primeros números compuestos (4, 6, 8, 9 y 10).Comprueba tus conocimientos.
Antes de empezar a resolver el test pincha en Instrucciones. Este test se compone de dos bloques de cinco emparejamientos cada uno. Javascript original de Alejandro ValeroA continuación puedes aplicar las reglas de divisibilidad a los 6 siguientes números de cuatro cifras escribiendo en cada caso si o no (con minúsculas, sin acento) en cada casilla según corresponda. Cuando acabes pulsa el botón comprobar para ver si lo has hecho bien.