XIV Olimpiada Matemática 2º E.S.O. Individual

Sociedad Madrileña de Profesores de Matemáticas

Problemas que se han propuesto para resolución individual

Fase semifinal de la XIV Olimpiada Matemática para 2º de la E.S.O. de la Comunidad de Madrid. Miércoles, 26 de abril de 2006. Prueba individual.
(10/02/07) Actualización: Colocadas las soluciones.


Tened en cuenta que al resolver un problema, el proceso que hayáis seguido para llegar al resultado es tan importante como él mismo. Por ello os pedimos que al final deis la solución que hayáis encontrado y también que expliquéis cuáles fueron las ideas más importantes que os llevaron hasta ella.


PLEGANDO CUBOS
La siguiente figura muestra el desarrollo plano de un cubo en el que hemos trazado diferentes líneas en cada una de sus caras.


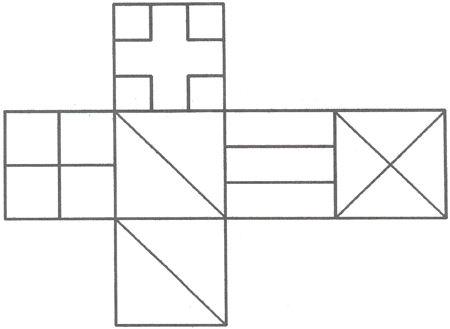
Desarrollo del cubo

Indica cuáles de los siguientes cubos se pueden construir a partir de la figura anterior.

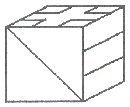
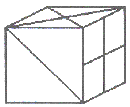
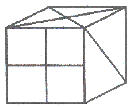
Cubo 1 Cubo 2 Cubo 3

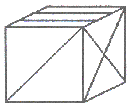
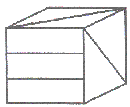
Cubo 4 Cubo 5

NUMERANDO CASAS
En una urbanización de los alrededores de Madrid, se numeran las casas con unos pequeños ladrillos de cerámica muy bonitos que tienen cada uno una cifra, de forma que para colocar el número 25 hay que colocar dos ladrillos, el del 2 y el del 5.
En la urbanización hay 87 casas, que queremos numerar en orden correlativo desde el 1 al 87.
a. ¿Cuántos ladrillos con el número 6 necesitaremos?
b. ¿Y ladrillos con el 9?
c. ¿Cuántos ladrillos necesitaremos en total?
d. ¿Cuánto sumarán todos los 4 que haya en los ladrillos empleados?

LAS PÁGINAS DEL LIBRO
Un escritor ha escrito dos libros, que suman entre los dos 356 páginas. Cada libro tiene un formato diferente. Las dimensiones de las hojas del primero es de 20 cm de largo y 15 cm de ancho, mientras que las del segundo libro son de 17 cm de largo y 12 cm de ancho.
Si se extendieran las hojas de los libros, la superficie que cubrirían sería 4 metros2 y 1400 cm2.
Teniendo en cuenta estos datos, ¿cuántas páginas tiene cada libro?

CEROS
Determina en cuántos ceros termina el producto:


25×25 x 25×25 x 25×25 x 25×5 x 8×8

Explica la solución y realiza el ejercicio sin calculadora y sin hacer el algoritmo de la multiplicación.

SOLUCIONES


PLEGANDO CUBOS
La siguiente figura muestra el desarrollo plano de un cubo en el que hemos trazado diferentes líneas en cada una de sus caras.

Desarrollo del cubo

Indica cuáles de los siguientes cubos se pueden construir a partir de la figura anterior.

Cubo 1 Cubo 2 Cubo 3

Cubo 4 Cubo 5


Todos, salvo el tercero, corresponden a diferentes vistas del cubo cuyo desarrollo viene dado.

NUMERANDO CASAS
En una urbanización de los alrededores de Madrid, se numeran las casas con unos pequeños ladrillos de cerámica muy bonitos que tienen cada uno una cifra, de forma que para colocar el número 25 hay que colocar dos ladrillos, el del 2 y el del 5.
En la urbanización hay 87 casas, que queremos numerar en orden correlativo desde el 1 al 87.
a. ¿Cuántos ladrillos con el número 6 necesitaremos?
b. ¿Y ladrillos con el 9?
c. ¿Cuántos ladrillos necesitaremos en total?
d. ¿Cuánto sumarán todos los 4 que haya en los ladrillos empleados?


Para resolver este problema, interesa hacer una partición de los números que vamos a emplear de la siguiente manera:

– Nueve números que corresponderán a los nueve primeros, es decir, del 1 al 9.
– Siete decenas completas formadas por números de dos cifras, la primera de ellas del 10 al 19 y la última del 70 al 79.
– Ocho números más de dos cifras, del 80 al 87.

a. Para saber cuántos ladrillos necesitamos del número 6:

– Del primer grupo:
- Casas del 1 al 9… un ladrillo con la cifra 6 (el de la casa 6)
– Del segundo grupo:
– Casas del 10 al 19…. un ladrillo con la cifra 6 (el de la casa 16)
– Casas del 20 al 29…. un ladrillo con la cifra 6 (el de la casa 26)
– Casas del 30 al 39…. un ladrillo con la cifra 6 (el de la casa 36)
– Casas del 40 al 49…. un ladrillo con la cifra 6 (el de la casa 46)
– Casas del 50 al 59…. un ladrillo con la cifra 6 (el de la casa 56)
– Casas del 60 al 69…. diez ladrillos con la cifra 6 más otro más (el de la casa 66)
– Casas del 70 al 79…. un ladrillo con la cifra 6 (el de la casa 76)
– Del tercer grupo:
- Casas del 80 al 87…. un ladrillo con la cifra 6 (el de la casa 86)

En total, se necesitan: 1 + 17 + 1 = 19 ladrillos con el número 6.

b. Para saber cuántos ladrillos necesitamos de número 9:

– Del primer grupo:
- Casas del 1 al 9… un ladrillo con la cifra 9 (el de la casa 9)
– Del segundo grupo:
– Casas del 10 al 19…. un ladrillo con la cifra 9 (el de la casa 19)
– Casas del 20 al 29…. un ladrillo con la cifra 9 (el de la casa 29)
– Casas del 30 al 39…. un ladrillo con la cifra 9 (el de la casa 39)
– Casas del 40 al 49…. un ladrillo con la cifra 9 (el de la casa 49)
– Casas del 50 al 59…. un ladrillo con la cifra 9 (el de la casa 59)
– Casas del 60 al 69…. un ladrillo con la cifra 9 (el de la casa 69)
– Casas del 70 al 79…. un ladrillo con la cifra 9 (el de la casa 79)
– Del tercer grupo:
– Casas del 80 al 87…. ningún ladrillo con la cifra 9

En total, se necesitan: 1 + 7 = 8 ladrillos con el número 9.

c. Para saber cuántos ladrillos se necesitan en total:
– Del primer grupo:

– Casas del 1 al 9…. nueve ladrillos

– Del segundo grupo:
– Casas del 10 al 19…. diez números de dos cifras… veinte ladrillos
– Casas del 20 al 29…. diez números de dos cifras… veinte ladrillos
– Casas del 30 al 39…. diez números de dos cifras… veinte ladrillos
– Casas del 40 al 49…. diez números de dos cifras… veinte ladrillos
– Casas del 50 al 59…. diez números de dos cifras… veinte ladrillos
– Casas del 60 al 69…. diez números de dos cifras… veinte ladrillos
– Casas del 70 al 79…. diez números de dos cifras… veinte ladrillos
– Del tercer grupo:
– Casas del 80 al 87…. ocho números de dos cifras… dieciséis ladrillos

En total, se necesitan: 9 + 7×20 + 16 = 9 + 140 + 16 = 165 ladrillos

d. Para saber cuánto sumarán los todos los 4 que haya en los ladrillos empleados:

Un razonamiento totalmente análogo al seguido en el apartado a. nos llevará a que la cantidad de ladrillos con el número 4 que se necesitan para numerar todas las casas es de 19. Por lo tanto, la suma de todos ellos será: 4×19 = 76.

LAS PÁGINAS DEL LIBRO
Un escritor ha escrito dos libros, que suman entre los dos 356 páginas. Cada libro tiene un formato diferente. Las dimensiones de las hojas del primero es de 20 cm de largo y 15 cm de ancho, mientras que las del segundo libro son de 17 cm de largo y 12 cm de ancho.
Si se extendieran las hojas de los libros, la superficie que cubrirían sería 4 metros2 y 1400 cm2.
Teniendo en cuenta estos datos, ¿cuántas páginas tiene cada libro?


Teniendo en cuenta que cada hoja tiene dos páginas: 356 : 2 = 178 hojas
4 m2 = 40000 cm2
Superficie total = 40000 + 1400 = 41400 cm2
Sea X el número de hojas del primer libro.
El segundo libro tendrá 178 – X hojas.
Podremos plantear la siguiente ecuación:
20×15 x X + 17×12 x (178 – X ) = 41400
De la que se obtiene que X = 53
Luego el primer libro tiene 53 hojas y el segundo 178 – 53 = 125
Pero como nos piden el número de páginas:
Solución: El primer libro tiene 106 páginas y el segundo 250.


CEROS
Determina en cuántos ceros termina el producto:


25×25 x 25×25 x 25×25 x 25×5 x 8×8

Explica la solución y realiza el ejercicio sin calculadora y sin hacer el algoritmo de la multiplicación.


Partiremos de la descomposición en factores primos de la expresión:
52 x 52 x 52 x 52 x 52 x 52 x 52 x 5 x 23 x 23 = 515 x 26 = 106 x 59
El número acabará en seis ceros pues son los que habrá que añadir al resultado de 59 que no acaba en cero sino en cinco.


Texto de Ángel Puente - 26.04.06

URL del artículo: http://www.tinglado.net/?id=xiv-olimpiada-matematica-2-eso-individual

(El tinglado - http://www.tinglado.net - Con licencia de Creative Commons)